Filosofía y Educación

Descargar artículo

La lógica es la técnica directiva de la razón humana por medio de la cual ésta procede de manera ordenada y sin error.

El conocimiento humano empieza por los sentidos (vista, oído, tacto, gusto, dolor...) y por las representaciones sensibles (imágenes, recuerdos...), pero se remonta al ámbito del entendimiento, de la inteligencia. Es el que llamamos conocimiento racional, formado por ideas o conceptos y por las relaciones que se establecen entre ellas (juicios, razonamientos).

El conocimiento sensible nos ofrece datos e imágenes concretos y singulares de los objetos, de las cosas: Veo esta manzana, con este color determinado, este tamaño, tiene este sabor concreto...

El conocimiento racional, en cambio, es una representación abstracta y universal de los objetos de la realidad: la idea o concepto de manzana no se reduce a “esta” manzana concreta, con tal tamaño y forma..., sino a lo que es propio de toda manzana, a la esencia de “manzana”, a lo que significa ser una manzana y no una naranja o un martillo o un gato...

El saber propiamente humano es el ofrecido por el conocimiento racional, por la inteligencia. A este, a sus leyes y propiedades a la hora de ser utilizado con corrección y precisión, es al que se refiere la lógica.

I) Las elaboraciones propias del conocimiento racional o intelectual son las ideas o conceptos.

El concepto es la representación intelectual de un objeto.

Un concepto es un signo, es decir, algo que representa a otra cosa distinta. Hay dos tipos de signos (o señales): los signos naturales y los artificiales.

Los naturales nos remiten de suyo, por sí mismos, al objeto al que representan, porque guardan con él alguna relación más o menos directa o evidente. Por ejemplo, el humo es signo del fuego, el dolor físico es signo o señal de algún tipo de disfunción o malestar orgánico, psicológico o de otro tipo. El concepto o idea es un signo natural de aquello que representa.

Los signos artificiales no guardan por sí mismos una relación evidente con lo representado. Son convencionales o arbitrarios. Por ejemplo, los colores de un semáforo, una bandera o un himno, o cualquier otra señal convencional (las señales del mus, el lenguaje Braille, etc.) Los signos artificiales también se llaman símbolos.

Un concepto tiene dos elementos: la comprensión y la extensión.

La comprensión es el conjunto de notas o características que constituyen un concepto; designa la esencia o modo de ser de lo representado. Así:

• “navarro”: aquél que ha nacido o reside en Navarra
• “hombre”: animal racional
• “cuadrado”: polígono formado por cuatro lados

La extensión se refiere al número de individuos a los que se aplica el concepto. En los ejemplos anteriores, sería en cada caso el conjunto de individuos a los que afecta el ser “navarros”, ser “hombres” o ser “cuadrados”. La comprensión indica lo que son esos individuos; la extensión indica cuántos son.

Pues bien, cuantas más notas o características comprende un concepto, más restringido es el número de los individuos a los que afecta. Cuanto mayor es la comprensión, menor es la extensión; y a menor comprensión –menos características que cumplir-, mayor extensión, más individuos caben dentro de ese concepto.

Por ejemplo: Hay más felinos que gatos, porque la comprensión del concepto felino es menor -incluye menos condiciones- que la de ser gato. Ser asturiano implica algo más que ser meramente español, incluye una restricción: el haber nacido (o vivir) en Asturias, cosa que los demás españoles no cumplirían. Y por eso el número de asturianos es inferior. Son menos los que cumplen el conjunto de condiciones que definen a los asturianos.

Las propiedades del concepto son dos: la universalidad y la abstracción.

• Universal significa que se refiere a muchos objetos posibles (a todos los del mismo tipo).
• Abstracto significa que no está vinculado necesariamente a unas características sensibles concretas.

Así, el concepto de “isla” se refiere a todas las islas existentes o posibles (universalidad). Y ello sin que las peculiaridades sensibles de esas islas excluyan a ninguna: las grandes lo mismo que las pequeñas, las montañosas igual que las llanas, las habitadas y las deshabitadas, las pobladas de vegetación lo mismo que las desérticas, etc. (abstracción)

II) Pasemos ahora a hablar del término. Término, en principio, viene a ser lo mismo que palabra.

Término es la expresión verbal (oral o escrita) de un concepto.

Los términos son signos artificiales, símbolos. Se deciden de forma convencional o arbitraria. (La misma idea, por ejemplo “domingo”, es expresada con palabras diferentes según los idiomas, de acuerdo con las convenciones lingüísticas de cada caso: dimanche, sunday... A la misma idea le corresponden palabras distintas, que no obstante se pueden traducir entre sí porque se refieren a lo mismo.) Las ideas son signos naturales y las palabras o términos son signos convencionales o artificiales.

División de los términos

a) Por el tipo de símbolo: Términos simples, los que se expresan con una sola palabra (perro, piedra, león...) Términos compuestos, los que se expresan más de una palabra (azul claro, vino añejo, libro de Matemáticas, Ciudad Real, etc.)

b) Por su significado:

• Unívocos: los que se usan con un solo significado. P. ej., Botella, bolígrafo, puerta, etc.
• Análogos: los que se usan con significados en parte iguales y en parte distintos. P. ej., sano (en referencia una persona que tiene buena salud, a un alimento que está en buenas condiciones, a un color que indica que posee buena salud, etc.); seguro(aplicado a un edificio, un puente u otra construcción, denotando que es sólido, no ofrece peligro, no se va a caer...; a un argumento, porque no ofrece dudas...; a un amigo, porque se puede confiar en él, etc.)
• Equívocos: los que se usan con sentidos completamente diferentes. P. ej., vaca, que puede significar al animal pero también, fonéticamente (“baca”), a la parrilla que se coloca sobre los vehículos para transportar utensilios o maletas; tajada: parte o fragmento de un alimento, pero también borrachera.

Volver al índice

I) EL JUICIO LÓGICO.

Juicio es un pensamiento (representación intelectual) en el cual se afirma o se niega algo.

P. ej.: “El libro de matemáticas está muy bien ilustrado”
“Costa Rica es un país americano”.

• Es una combinación de conceptos, que se ponen en relación.
• Alude o representa un acontecimiento real (algo que ocurre, que “es así”)

Elementos del juicio:

• Sujeto: concepto del que se afirma o se niega.
• Predicado: concepto afirmado o negado.
• Cópula: elemento que enlaza y relaciona al sujeto y al predicado

II) LA PROPOSICIÓN O ENUNCIADO.

La proposición es la expresión verbal de un juicio.

Tipos de proposiciones:

a) Por la clase de cópula:

• Simples: “S es P”: Pedro es madrileño.
• Compuestas: Enlazan dos simples. Pueden ser: Conjuntivas (“y”): Pedro es madrileño y escultor; alternativas o disyuntivas (“o”): Esta tarde iré al cine o me quedaré leyendo; y condicionales (“si... entonces”): Si vienes, daremos una vuelta.

b) Por la cantidad (según la extensión con la que se toma el sujeto):

• Universales: El paramecio es un ser unicelular.
• Particulares: Algunos alumnos son roncaleses.
• Singulares: Beatriz acaba de cumplir 16 años.

(Cuando las proposiciones forman parte de una argumentación o razonamiento, las universales y las singulares se comportan de la misma manera, ya que se toma el sujeto en toda su extensión. Esto es muy importante a la hora de elaborar razonamientos para no incurrir en falacias o errores de argumentación.)

c) Por la cualidad (según que afirmen o nieguen)

• Afirmativas: María vendrá de París el jueves.
• Negativas: Ningún conocido mío es político.

En función de estas dos últimas divisiones se clasifican las proposiciones en cuatro tipos fundamentales:

Se pueden representar gráficamente por medio de los llamados Diagramas de Euler:

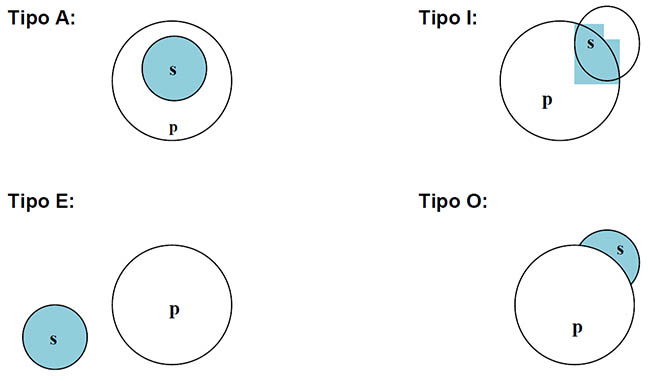
Es importante advertir que:

• EN TODA PROPOSICIÓN AFIRMATIVA, EL PREDICADO SE TOMA PARTICULARMENTE
• EN TODA PROPOSICIÓN NEGATIVA, EL PREDICADO SE TOMA UNIVERSALMENTE.

LA OPOSICIÓN DE LAS PROPOSICIONES

Se llaman proposiciones opuestas las que, teniendo los mismos sujeto y predicado, difieren en cantidad, en cualidad o en ambas cosas a la vez.

“Cuadrado lógico de la oposición”

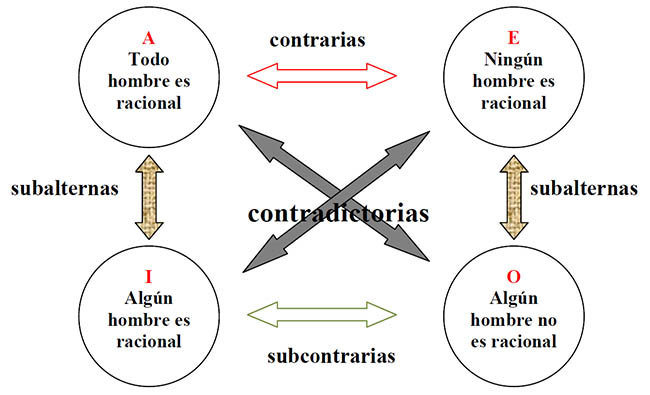
Formas de oposición:

A) Proposiciones CONTRADICTORIAS: Difieren en cantidad y cualidad.

“Algún músico es rockero” ( I ) - “Ningún músico es rockero” ( E )

Tienen de particular que no pueden ser verdaderas ni falsas a la vez: Si una es verdadera, la otra es falsa, y viceversa.

B) Proposiciones CONTRARIAS: Proposiciones universales que difieren en la cualidad.

“Todo músico es rockero” (A) - “Ningún músico es rockero” (E)

No pueden ser verdaderas a la vez; pero sí falsas a la vez. Si una es verdadera, la otra es falsa. Pero si una es falsa, la otra puede ser verdadera o falsa.

C) Proposiciones SUBCONTRARIAS: Proposiciones particulares que difieren en cualidad.

“Algún músico es rockero” (I) - “Algún músico no es rockero” (O)

No pueden ser falsas a la vez, pero sí verdaderas a la vez. Si una es falsa, l a otra es verdadera; pero si una es verdadera, la otra puede ser verdadera o falsa.

D) Proposiciones SUBALTERNAS: Proposiciones de igual cualidad, pero diferentes en cantidad.

“Todo músico es rockero” (A) - “Algún músico es rockero” (I)

Cuando la particular es falsa, la universal también; y cuando la universal es verdadera, la particular también. Pero no a la inversa.

La conversión de proposiciones

Con el fin de no incurrir en argumentaciones falaces, se ha estudiado la relación entre los términos en función del lugar que ocupan: sujeto o predicado, recordando que la cantidad de los términos no es la misma en un caso y en el otro: como ya se dijo, en las proposiciones afirmativas el predicado se toma siempre de modo particular, mientras que en las negativas el predicado es tomado siempre universalmente.

Conversión es la operación lógica que consiste en invertir
los extremos de una proposición (sujeto y predicado) de manera que,
sin variar la cualidad, se mantenga el valor de verdad.

Existen tres tipos de conversión: simple, por accidente y por contraposición. Nosotros sólo vamos a ver aquí las dos primeras.

Conversión simple:

- No varía ni la cantidad ni la cualidad. Sólo es legítima en las proposiciones de tipo E y en las de tipo I.

Ningún hombre es sabio «——» Ningún sabio es hombre

Algún hombre es sabio «——» Algún sabio es hombre

Conversión por accidente:

Varía la cantidad, pero no la cualidad (y si una es verdadera, su conversa también).

Sólo es legítima en el caso de las proposiciones de tipo E y A.

Todo hombre es mamífero «——» Algún mamífero es hombre ( I )

Ningún mamífero es reptil «——» Algún reptil no es mamífero ( O )

Volver al índice

I. RAZONAMIENTO Y DISCURSO O ARGUMENTACIÓN

Razonamiento es un pensamiento complejo por el que,
a partir de algún juicio dado, se obtiene otro nuevo.
La expresión verbal del razonamiento es la argumentación o discurso.

Hay dos tipos de razonamiento:

- inducción o razonamiento inductivo
- y deducción o razonamiento deductivo

La inducción es un razonamiento mediante el cual, a partir de datos singulares o particulares, se obtiene una proposición universal.

Ejemplo: La tiza cae con una aceleración de 9’8 m/seg., luego los cuerpos caen con una aceleración de 9’8...

Tipos de inducción:

• Completa: Parte de la enumeración completa de todos los datos singulares o particulares que integran la conclusión.
  Ejemplo: Lunes, martes, miércoles, jueves, viernes, sábado y domingo tienen 24 horas; luego los días de la semana tienen 24 horas.
• Incompleta: Parte de una enumeración incompleta pero suficiente.
  Ejemplo: Fe, cobre, Ni, mercurio son buenos conductores del calor. Luego los metales son buenos conductores del calor.

La inducción es un razonamiento mediante el cual, a partir de datos singulares o particulares, se obtiene una proposición universal.

Ejemplo: La tiza cae con una aceleración de 9’8 m/seg., luego los cuerpos caen con una aceleración de 9’8...

Tipos de inducción:

• Completa: Parte de la enumeración completa de todos los datos singulares o particulares que integran la conclusión.
  Ejemplo: Lunes, martes, miércoles, jueves, viernes, sábado y domingo tienen 24 horas; luego los días de la semana tienen 24 horas.
• Incompleta: Parte de una enumeración incompleta pero suficiente.
  Ejemplo: Fe, cobre, Ni, mercurio son buenos conductores del calor. Luego los metales son buenos conductores del calor.

La deducción es un razonamiento mediante el cual, de una proposición más universal se llega a una proposición menos o igual de universal.
Ejemplo: Todo hombre es animal; Joaquín es hombre, luego Joaquín es animal.

II. EL SILOGISMO

Es la expresión verbal de un razonamiento deductivo

Tipos de silogismo:

• Silogismo categórico, que consta de tres proposiciones simples:

Todos los personajes de ficción son figuras ejemplarizantes
Don Quijote es un personaje de ficción
Luego Don Quijote es una figura ejemplarizante

• Silogismo hipotético, que parte de una proposición compuesta (conjuntiva, alternativa o condicional):

O es de día o es de noche
es de día,
luego no es de noche.

Las proposiciones a partir de las cuales se deduce, se llaman PREMISAS, y la proposición a la que se llega como resultado se llama CONCLUSIÓN.

Volver al índice

[A partir de ahora, salvo advertencia, nos referiremos a él simplemente como “silogismo”.]

Silogismo es la expresión verbal de un razonamiento deductivo

Recordemos que el razonamiento deductivo es aquel en el que, de una proposición más universal se obtiene una proposición menos o igual de universal que ella.

Es preciso distinguir, previamente, entre dos tipos de silogismo:

• Silogismo categórico, que consta de tres proposiciones simples:

Todos los personajes de ficción son figuras ejemplarizantes
Don Quijote es un personaje de ficción
Luego Don Quijote es una figura ejemplarizante

• Silogismo hipotético, que parte de una proposición compuesta (conjuntiva, alternativa o condicional):

O es de día o es de noche
es de día,
luego no es de noche.

Las proposiciones a partir de las cuales se deduce, se llaman PREMISAS, y aquella a la que se llega como resultado se llama CONCLUSIÓN.

1. EL SILOGISMO CATEGÓRICO

Nos vamos a centrar primero en el estudio del silogismo categórico. En él se parte de la identificación de dos términos con un tercero para concluir a partir de ahí la identificación de aquellos términos entre sí.

Materia del silogismo categórico

a) Materia remota: Son los términos que, comparados dos a dos, forman el silogismo. Se llaman “extremos” (menor y mayor) y “término medio”.

• Término menor: es el sujeto de la conclusión (s)
• Término mayor: es el predicado de la conclusión (p)
• Término medio: es el término común a las premisas, que compara a los términos Mayor y menor sin entrar con ellos en la conclusión (m)

b) Materia próxima: Son las proposiciones de las que consta el silogismo. Se llaman premisas y conclusión:

• Premisa mayor: es aquella en la que aparece el término mayor (p)
• Premisa menor: aquella en la que aparece el término menor (s)
• Conclusión: proposición que se sigue o se obtiene de las premisas.

En el silogismo, la conclusión se sigue necesariamente de las premisas.

Advertencia: Para proceder con orden, se ha adoptado el criterio de colocar siempre la premisa mayor en primer lugar.

Forma del silogismo categórico

Es la estructura lógica por la cual, a partir de la identificación con un término común (m), se obtiene el enlace de dos términos distintos (s - p). Así, por ejemplo, la disposición de los términos en las premisas determinará la conclusión que se obtiene.

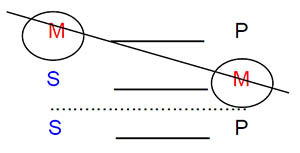
Dicha estructura se recoge en una serie de principios y de reglas del silogismo.

Principios reguladores del silogismo:

REGLAS DEL SILOGISMO:

Todo silogismo correcto ha de basarse también en las siguientes reglas. Cuatro corresponden a los términos y cuatro a las proposiciones.

1) Reglas para los términos:

El perro es un mamífero canino / el gato es un mamífero felino —> ¿?

Todo sabio es paciente / todo sabio es culto —> ¿Todo culto es paciente?

(¿Y los posibles cultos que no son sabios?...)

Obsérvese que “culto” es universal en la conclusión, pero en la premisa menor es particular, ya que es predicado de una proposición afirmativa.

Napoleón era corso / Napoleón era emperador —> ¿Napoleón...?

(De lo contrario se faltaría a la R.1. Puede ocurrir que la ‘parte’ de M que afecta a la primera premisa no sea la misma que la que afecta a la 2ª)

Las piedras son pesadas / Las maderas son pesadas —> ¿Las maderas son piedras...?

Reglas para las proposiciones:

(Por el principio de conveniencia)

(Porque al negar la relación con el término medio se niega toda relación entre el mayor y el menor. Sujeto y predicado no tienen nada que ver entre sí)

Las serpientes no son mamíferos / Los cetáceos no son serpientes —> ¿?

a) Si una premisa es negativa: se niega uno de los extremos (S, P) respecto del término medio. Por lo tanto, no pueden aquéllos convenir entre sí (Principio de discrepancia). Y la conclusión es negativa.

b) Si una premisa es particular:

3 posibilidades:

• Primera: Ambas premisas afirmativas. Sus predicados son particulares; y también el sujeto de una premisa (por la hipótesis que manejamos). El sujeto de la otra premisa debe ser el término medio (por R.4), que debe ser universal y no entra en la conclusión (R. 3); y además, por R.2, en la conclusión ningún término puede tener más extensión que en las premisas. Luego el sujeto de la conclusión tiene que ser particular.
• Segunda: Ambas premisas negativas. Por R.6 no pueden concluir.
• Tercera: Una premisa afirmativa y otra negativa. Por hipótesis, el sujeto de una premisa es particular, y el predicado de la afirmativa también. Por lo tanto, sólo quedan dos términos que pudieran ser universales. De ellos, uno ha de ser el término medio (R.4), y el otro el término mayor (predicado de la conclusión, que ha de ser negativa, por la 1ª parte de esta regla). Por consiguiente, el término menor, sujeto de la conclusión, no puede ser universal sino particular.

Ejemplos:

• Todos los reptiles son de sangre fría / Algunos animales domésticos son reptiles. Luego algunos animales domésticos son de sangre fría.
• Ningún analfabeto sabe hacer análisis sintácticos / Algunos alumnos saben hacer análisis sintácticos. Luego algunos alumnos no son analfabetos.

3 posibilidades:

• Primera: Ambas premisas afirmativas. Por hipótesis, los sujetos de las dos premisas son particulares. Pero si son ambas afirmativas, se falta contra la R. 4. Se descarta, así pues, esta posibilidad.
• Segunda: Ambas premisas negativas. No concluye, por R.6.
• Tercera: Una premisa afirmativa y la otra negativa. Si una premisa es negativa y otra afirmativa, sólo puede haber un término universal, el predicado de la negativa, que por fuerza ha de ser el término medio (R.4). Por R.7, la conclusión tiene que ser particular y negativa, y el predicado de ésta ha de ser universal; pero en las premisas el único término universal era el término medio, que no puede entrar en la conclusión. Por consiguiente, no concluye.

Ejemplo: Algunos hombres son paralíticos / Algunos hombres son laboriosos... —> ¿?

Figuras y modos del silogismo categórico

1) Figuras del silogismo son las diferentes disposiciones del silogismo según la colocación del TÉRMINO MEDIO (disposición de la materia remota)

Hay cuatro figuras:

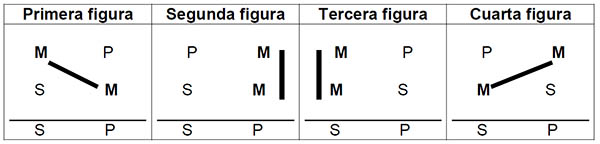
2) Modos del silogismo son las distintas combinaciones que pueden hacerse con las premisas y la conclusión, atendiendo a su cantidad y cualidad (disposición de la materia próxima)

De un total de 256 combinaciones posibles, sólo 19 de ellas son modos legítimos, los cuales se clasifican según las cuatro figuras, de este modo. Además hay 5 conclusiones “debilitadas”.

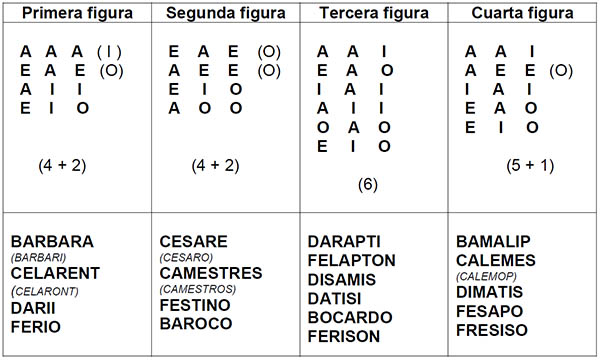
Con el fin de recordar los MODOS LEGÍTIMOS del silogismo, se han inventado unas palabras mnemotécnicas, que aparecen en la parte inferior de cada figura.

Reducción de los modos a la Primera Figura

La primera figura del silogismo categórico es la que presenta un mayor grado de evidencia intuitiva. Además, en ella se dan los cuatro tipos de conclusión (A,E,I,O). Esto llevó a los lógicos a intentar reducir todos los modos legítimos a los de la primera figura. Se trata de convertir un silogismo de la 2ª, la 3ª o la 4ª figuras en otro equivalente de la 1ª.

Ello se puede hacer por medio de dos tipos de reducción: la reducción directa(también llamada perfecta) y la reducción al absurdo. Nosotros sólo estudiaremos la primera de ellas.

Para reducir un silogismo por medio de la reducción directa se busca razonar en primera figura y llegar a la misma conclusión. Esto es posible en todos los casos menos en BAROCO Y BOCARDO (que sí admiten la reducción al absurdo).

Para ello se efectúan dos posibles operaciones:

1. CONVERSIÓN de una de las premisas o de la conclusión.
2. MUTACIÓN de las premisas.

Lo primero que hay que tener en cuenta es la CONSONANTE INICIAL (B, C, D, F) del silogismo con el que estamos trabajando, y que señala el modo de la primera figura al que hay que reducirlo.

Después, hay que observar si la palabra que designa al silogismo incluye las consonantes S, P, M, que indican la operación que hay que realizar con la proposición representada por la vocal que las precede:

Ejemplos:

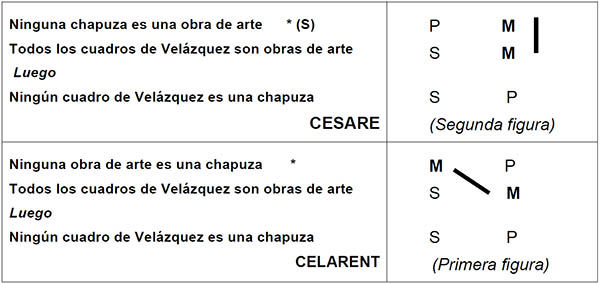
1) Ninguna chapuza es una obra de arte
Todos los cuadros de Velázquez son obras de arte

Luego Ningún cuadro de Velázquez es una chapuza

(Es un CESARE)

La palabra CESARE indica que hay que reducirlo a CELARENT, en la primera figura. Y también que hay que efectuar una conversión simple (S) de la premisa mayor:

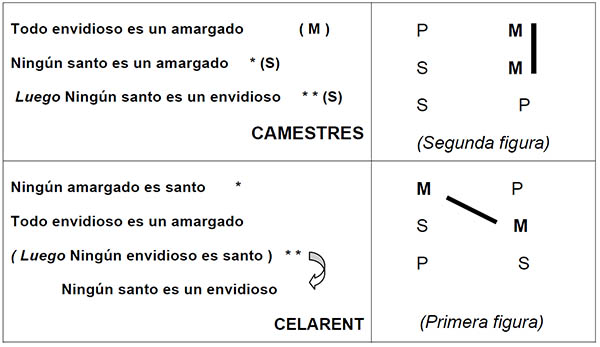
2) Todo envidioso es un amargado
Ningún santo es un amargado

Luego Ningún santo es un envidioso

(Es un CAMESTRES)

La palabra CAMESTRES indica que hay que reducirlo a CELARENT, en la primera figura. Y también que hay que efectuar una MUTACIÓN DE PREMISAS, una conversión simple (S) de la premisa menor, y una conversión simple de la conclusión:

2. EL SILOGISMO HIPOTÉTICO

Es el silogismo que parte de una proposición compuesta (conjuntiva, alternativa o condicional), que es la premisa mayor, y cuya premisa menor establece o destruye uno de los miembros.

1) El silogismo conjuntivo

Es aquél cuya premisa mayor es una proposición CONJUNTIVA, afirmativa o negativa.

a) A partir de la afirmativa, en el silogismo se deduce uno u otro de sus miembros:

Llueve y hace sol
Luego llueve / Luego hace sol

b) En la negativa se niega que dos proposiciones puedan ser verdaderas al mismo tiempo. Y, así, en la mayor se niega la conjunción; en la menor se afirma uno de los dos miembros, y se concluye con la negación del otro:

Pedro no duerme y estudia (a la vez)
(o bien: No es posible que Pedro duerma y estudie a la vez)

Pedro duerme
Luego no estudia

ESTA ES LA FIGURA LLAMADA ‘PONENDO TOLLENS’: Se afirma en la premisa menor (ponendo) para negar en la conclusión (tollens)

¡¡ Pero de la negación de un miembro no se sigue la afirmación del otro!!: (Pedro podría no dormir ni estudiar)

2) El silogismo disyuntivo (exclusivo)

Es el silogismo hipotético cuya premisa mayor es una proposición alternativa (disyuntiva), y cuya premisa menor afirma o niega uno de los miembros alternativos, para negar o afirmar, respectivamente, el otro en la conclusión.

O tenemos un gobernante, o mandamos todos.

El silogismo disyuntivo, así entendido, admite dos casos diferentes (o FIGURAS):

A) PONENDO TOLLENS: La mayor es una alternativa, la menor afirma un miembro (ponendo) y la conclusión niega el otro (tollens): “Tenemos gobernante, luego no mandamos todos”.

B) TOLLENDO PONENS: La mayor es una alternativa, la menor niega un miembro (tollendo) y la conclusión afirma el otro (ponens): “No tenemos gobernante, luego mandamos todos”.

Se admite también otra forma de silogismo disyuntivo, INCLUSIVO, en el que la alternativa no excluye la verdad simultánea de ambos miembros. (P. ej.: Esta tarde lloverá o hará frío...)

3) El silogismo condicional

Es aquél cuya premisa mayor es una proposición condicional, y cuya premisa menor afirma o niega uno de los miembros (llamados antecedente y consecuente).

Si Pedro actuó entonces con serenidad, era un valiente
Pedro actuó entonces con serenidad
Luego es un valiente

Son posibles dos casos o figuras:

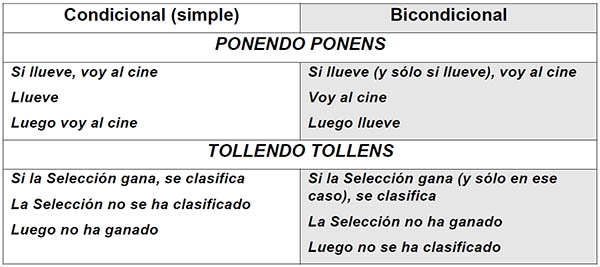
1. PONENDO PONENS: La menor afirma el antecedente y la conclusión afirma el consecuente.
2. TOLLENDO TOLLENS: La menor niega el consecuente y la conclusión niega el antecedente.

¡¡Pero de la negación del antecedente no se sigue la del consecuente; y de la afirmación del consecuente no se sigue la del antecedente!! Para estos dos casos, habría que establecer una condición más fuerte, del tipo “SI Y SÓLO SI...”, llamada BICONDICIONAL:

SILOGISMOS:
EJERCICIOS PRÁCTICOS

I) ¿Son correctos los silogismos y modos siguientes? ¿Por qué? Si es el caso, indica alguna regla contra la que atentan.

1. Los negros son seres humanos / Los Batusis son seres humanos / Luego los Batusis son negros
2. Los artesanos son profesionales muy valiosos / Algunos valencianos son artesanos / Luego los valencianos son profesionales muy valiosos
3. Los árboles no oxigenan la atmósfera por la noche / Los rosales no son árboles / Luego los rosales oxigenan la atmósfera por la noche
4. Algunos atletas se dopan para rendir por encima de sus posibilidades / Los corredores de cross son atletas / Luego los corredores de cross se dopan para rendir por encima de sus posibilidades
5. EIE / AIO / AOE / AOO en la 1ª figura / AEO / IEO / AAI / OOE / OAO / AAA en la 3ª figura

II) CONCLUIR, SI ES POSIBLE, INDICANDO FIGURA Y MODO:

1. Todos los deportes deben ser actividades educativas
   Todos los deportes son actividades saludables
2. Ningún mamífero es pájaro
   Algún mamífero es un animal que vuela
3. Toda persona ambiciosa es dañina
   Ningún hombre honrado es dañino
4. Ningún animal es responsable de sus actos
   Todo animal es un ser vivo
5. Algunos músicos de jazz son buenos músicos
   Los imitadores de Louis Amstrong son músicos de jazz
6. Todo lo que dignifica al hombre es bueno
   La esclavitud no dignifica al hombre
7. Varios futbolistas de mi equipo son poco humildes
   Todos los futbolistas de mi equipo son famosos
8. Ningún planeta emite luz propia
   Algunos astros que emiten luz propia son astros antiquísimos

III) CONCLUIR Y REDUCIR A LA PRIMERA FIGURA, SI ES POSIBLE:

1. Ningún astronauta es egipcio
   Elías es egipcio …
2. Ningún pintor es ciego
   Algún pintor toca la guitarra…
3. Los vanidosos son personas insoportables
   Las personas insoportables suelen tener manías …
4. Las bicicletas no contaminan
   La bicicleta es un vehículo …
5. El estudio ayuda a superarse
   El estudio es una actividad costosa …
6. Ningún esquimal es jugador de baloncesto
   Los Bulls son jugadores de baloncesto …
7. Algunos gimnastas son voluntariosos
   Todo gimnasta es ágil …
8. La acupuntura es una técnica oriental
   Algunas técnicas orientales ayudan a curarse …
9. Las drogas quitan la libertad
   Algunas drogas son ofertas tentadoras …
10. Ningún riojano es astronauta
    Algún ingeniero es astronauta …
11. Ningún astronauta es navarro
    Algún astronauta es ingeniero …
12. Los habitantes de Narnia son generosos
    Ningún egoísta es generoso …